Haskell refactoring and the dependent types

Haskell is designed as λ2ω language where terms depend on types: type polymorphism, type classes and families.

(image from the Fundamental Haskell book written by me)

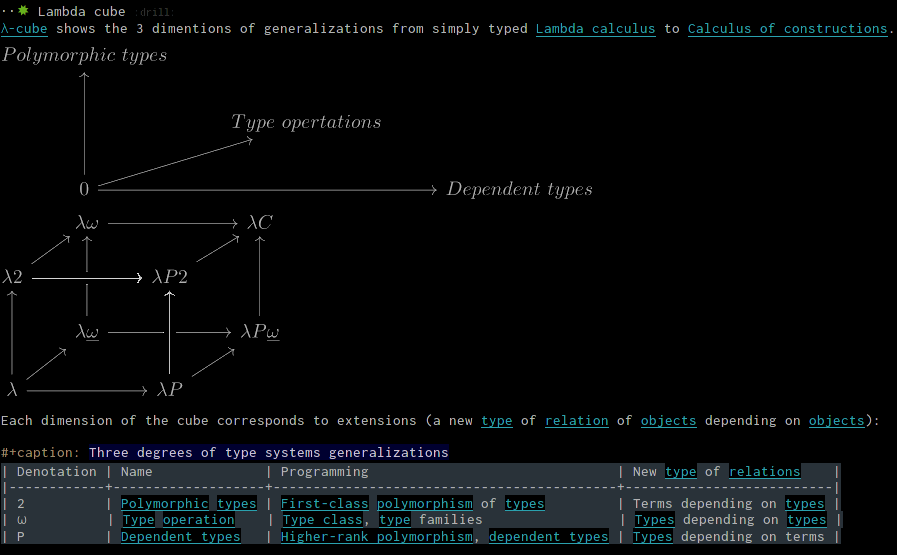
It is well-known that Dependently Typed code is not really reusable, because it contradicts with parametric polymorphism. And there is no discussion that it complicates the code, at least it raises the level of complexity of the code and requirements to other programmers, and complicates the type level management/programming especially at times in places where it ties-in with the regular λ2ω type system.

There is a number of extensions, for example, RankNTypes, DataKinds, and others that are really from the λP, λP2 spaces of Lambda Calculus where the types depend on terms.

The terms depend on types and types depend on terms are design contradiction, good design is about what was chosen to use and more importantly what was removed from the language design - good design is not "use everything at once".

"Perfection is achieved, not when there is nothing more to add, but when there is nothing left to take away."

Haskell λ2ω refactoring is easy and great to do. Classical Functional Programming Lisp-style refactoring is a key to good software design, parametric functions can be refactored/simplified into the form that by itself hints to the proper design of the code.

And some practical cases require the use of RankNTypes, DataKinds, and other λP features, and I agree they are areally powerful and sometimes needed.

Adding any λP uses into the code should be only where it is required. Adding the λP properties into the Haskell code makes the code really rigid (difficult to refactoring and extension). Because the main Haskell language and λP directly oppose by design. The reason the CoC is a vast research field - because of its infinite complexity and cases, it is more a mathematical research and proof space than programming space. So to keep the code clean flexible and extensible please try to minimize & localize the λP use and expose the classical λ2ω interfaces from the module. Don't be surprised that because of the λP use and introduced code rigidity, someone would have no other option left during refactoring or feature change but to rewrite the subsystem code all together with its interface, only because the subsystem got rigid by the use of the λP in λ2ω language.